11月12日分 復習と練習問題
1. 結晶に対して [ X線 ] を照射して得られる回折パターンは結晶の原子配列を知るために有用で,広く使われている.
2. 回折は,波長と結晶の格子面間隔との間に [ Bragg の回折条件 ] が成立するときにおこる.
3. X 線として波長 0.1937 nm の FeKα 線を用いて粉末X線回折を行った場合,NaCl の (111) 面からの回折は 2θ が何°のところに検出されるか.
まず (111) 面の面間隔 d を求める.塩化ナトリウムの格子定数を a とすると,簡単な幾何学的な計算により d = a/(√3) であることがわかる.
※とはいっても,ここがある意味一番難しいところでもある.(111) 面の面間隔を求めようとして,どこが面間隔かわからなかった人もいたようだ.たとえば下の図のように捉えると,面間隔は原点と原点に一番近い面 (濃い三角形で示された面) との距離なので,濃い三角形の重心と原点の間の距離を計算すればいいことがわかるのではないだろうか.
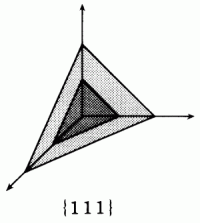
したがって a = 0.564 nm より,面間隔 d = 0.326 nm となる.
これを Bragg の式 2d sinθ = nλ に代入すると,n = 1 の回折線が sinθ= 0.2974,
すなわちθ=17.3°,2θ=34.6°に得られることになる.
下に実際の NaCl の粉末法X線回折パターンを示す.
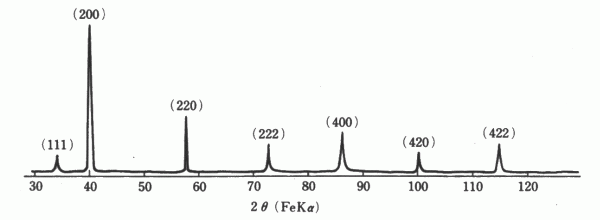
たしかに,計算値近辺に (111) 面からの回折ピークが観察されている.
4. 電子は加速電圧によって[ 波長 ]を変えることのできる波として取り扱え,結晶の回折パターンを得ることができる.加速電圧 10kV の電子線の波長を求めよ.
すこしまじめに波長と加速電圧の関係式を導いてみよう.
まず電子の運動エネルギーと加速電圧の関係を考える.電荷 qe を持つ電子は加速電圧 V で qeV のエネルギーを獲得する.これがすべて運動エネルギー (1/2)mv2 になるとすれば (m は電子の質量,v は運動速度),
(1/2)mv2=qeV
これを変形すると,
v = (2qeV/m)(1/2)・・・(1)
一方,電子の運動量 mv については de Bloigt の関係から
mv = h/λ ・・・(2)
(1),(2) 式から v を消去して λについて解くと,
λ={h2/(2mqeV)}(1/2) ・・・(3)
(3)式に数値 (h = 6.626×10-34 J s, qe = 1.602×10-19 C, m = 9.110×10-31 kg (電子の静止質量),V = 10×103 V) を代入して
λ = 0.01226 nm
が得られる.
ここで加速電圧が大きく,v が大きくなる場合には相対論効果を考えなくてはならないが,電子を 10kV 程度の電圧で加速する場合にはその影響は無視できるので (このまま計算すると v = 6×107 ms-1 と光速の 20% にすぎない),質量には静止質量をそのまま使っても問題ない.

